If you haven't been there, see Hint #1 first !  

Hopefully you've come to realize that water depth is the important variable for this kind of problem. For your calculations, an ideal world would be one in which water depth was uniform across the oceans, or at least uniform across broad stretches. However, bathymetric profiles often look something like this:

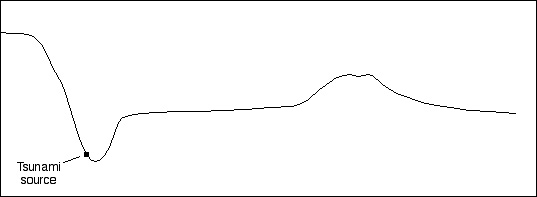
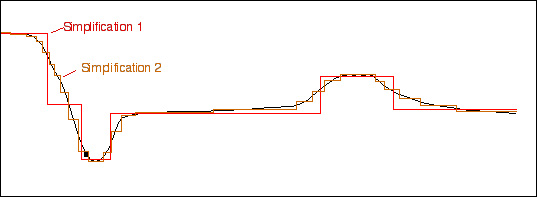
If we want to make our life simple, we can divide the profile up into segments. For a crude job, we can use a few segments (for example, something like Simplification 1 below), or for a more accurate treatment we can use something more like Simplification 2 (or, if we're really clever, we can use integral calculus, but that's another story).

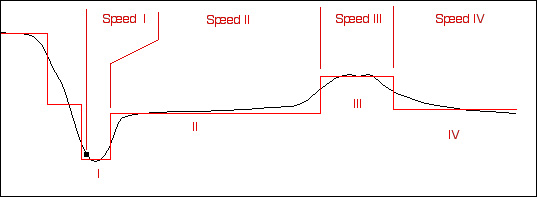
For the moment, let's use Simplification 1, which yields four intervals (n = I, II, III, and IV below). For each interval n, we can calculate the speed S(n) of the tsunami. Then we can calculate the travel time Time(n) = Distance(n) / Speed(n). Then we can add up the values of T(n) to get ΣT(n), which is the total travel time.

A good effort on this exercise will use more segments/intervals than Simplification 1.

The last thing about which you should think is what the speed of the tsunami will be over Interval IV in this example.  Newton's laws of motion, and/or the laws of thermodynamics, and/or some careful notes from lecture may be relevant to your considerations.

Contact your dutiful instructor if you have more questions!.

To the GEOL 3030 page.